|  |  |
|---|---|---|
 |  |  |
 |  |
Quick explanation of "what is a fractal"
The word “fractal” was invented in 1975 by the mathematician Benoit Mandelbrot. Until he took up the study of fractals, the sets were not important enough to require a term to denote them. But the existence of these patterns challenges us to study those forms that Euclid leaves aside as being “formless” to investigate the morphology of the “amorphous” (Mandelbrot, 1982). Mathematicians have preferred to study formally organised geometries rather than chaotic geometries of fractals.
Responding to this challenge, Mandelbrot conceived and developed a new geometry of nature and implemented its use in a number of diverse fields. For my dissertation I would like to investigate the application of fractal geometry in Architecture. Firstly we need to understand the significance of the word ‘fractal’.
Fractal word comes from the Latin adjective fractal. The corresponding Latin verb frangere means "to break": to create irregular fragments- that, in addition to "fragmented" fractus should also mean "irregular", both meanings being preserved in fragment. Therefore, the word fractal means to create irregular shapes from the breakage of fragments.
There is no definition of the term fractal accepted in the mathematician world. Mathematicians have therefore agreed a broad definition that many types of fractal geometry can be described with: “Natural phenomenon or a mathematical set that exhibits a repeating pattern that displays at every scale”. (Mandelbrot, 1982, p.58)
There are a lot of different types of fractals. Two of the most important properties of fractals are self-similarity and non-integer dimensions. (Mandelbrot, 1982)
If you look carefully at a fern leaf, you will notice that every little leaf - part of the bigger one - has the same shape as the whole fern leaf. You can say that the fern leaf is self-similar. The same self-similarity occurs with fractals: you can magnify them many times and after every step you will see the same shape, which is characteristic of that particular fractal.
Classical geometry deals with objects of integer dimensions: zero dimensional points, one dimensional lines and curves, two dimensional plane figures such as squares and circles, and three dimensional solids such as cubes and spheres. However, many natural phenomena are better described using a dimension between two whole numbers. So while a straight line has a dimension of one, a fractal curve will have a dimension between one and two, depending on how much space it takes up as it twists and curves. The more the flat fractal fills a plane, the closer it approaches two dimensions. (Mandelbrot, 1982)
FRACTAL
A New Look at the World: Fractal Geometry
Fractal geometry will make you see everything differently. There is a danger in reading further. You risk the loss of your childhood vision of clouds, forests, flowers, galaxies, leaves, feathers, rocks, mountains, torrents of water, carpet, bricks, and much else besides. Never again will your interpretation of these things be quite the same.
// currently working on Fractals //
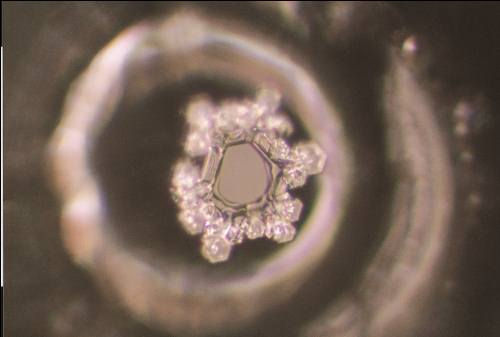
The Microscopic Structures of Dried Human Tears

Tears of joy, sadness, anger and hope under the microscope
In 2010, photographer Rose-Lynn Fisher published a book of remarkable images that captured the honeybee in an entirely new light. By using powerful scanning electron microscopes, she magnified a bee’s microscopic structures by hundreds or even thousands of times in size, revealing startling, abstract forms that are far too small to see with the naked eye.
Now, as part of a new project called “Topography of Tears,” she’s using microscopes to give us an unexpected view of another familiar subject: dried human tears.
"I started the project about five years ago, during a period of copious tears, amid lots of change and loss—so I had a surplus of raw material,” Fisher says. After the bee project and one in which she’d looked at a fragment of her own hip bone removed during surgery, she’d come to the realization that “everything we see in our lives is just the tip of the iceberg, visually,” she explains. “So I had this moment where I suddenly thought, ‘I wonder what a tear looks like up close?’”




When she caught one of her own tears on a slide, dried it, and then peered at it through a standard light microscope, “It was really interesting. It looked like an aerial view, almost as if I was looking down at a landscape from a plane,” she says. “Eventually, I started wondering—would a tear of grief look any different than a tear of joy? And how would they compare to, say, an onion tear?”
This idle musing ended up launching a multi-year photography project in which Fisher collected, examined and photographed more than 100 tears from both herself an a handful of other volunteers, including a newborn baby.
Scientifically, tears are divided into three different types, based on their origin. Both tears of grief and joy are psychic tears, triggered by extreme emotions, whether positive or negative. Basal tears are released continuously in tiny quantities (on average, 0.75 to 1.1 grams over a 24-hour period) to keep the cornea lubricated. Reflex tears are secreted in response to an irritant, like dust, onion vapors or tear gas.
All tears contain a variety of biological substances (including oils, antibodies and enzymes) suspended in salt water, but as Fisher saw, tears from each of the different categories include distinct molecules as well. Emotional tears, for instance, have been found to contain protein-based hormones including the neurotransmitter leucine enkephalin, a natural painkiller that is released when the body is under stress.
Additionally, because the structures seen under the microscope are largely crystallized salt, the circumstances under which the tear dries can lead to radically dissimilar shapes and formations, so two psychic tears with the exact same chemical makeup can look very different up close. “There are so many variables—there’s the chemistry, the viscosity, the setting, the evaporation rate and the settings of the microscope,” Fisher says.
As Fisher pored over the hundreds of dried tears, she began to see even more ways in which they resembled large-scale landscapes, or as she calls them, “aerial views of emotion terrain.”
“It’s amazing to me how the patterns of nature seem so similar, regardless of scale,” she says. “You can look at patterns of erosion that are etched into earth over thousands of years, and somehow they look very similar to the branched crystalline patterns of a dried tear that took less than a moment to form.”
Closely studying tears for so long has made Fisher think of them as far more than a salty liquid we discharge during difficult moments. “Tears are the medium of our most primal language in moments as unrelenting as death, as basic as hunger and as complex as a rite of passage,” she says. “It’s as though each one of our tears carries a microcosm of the collective human experience, like one drop of an ocean.”
Water memory
What is the photograph of frozen water crystals?
by Masaru Emoto
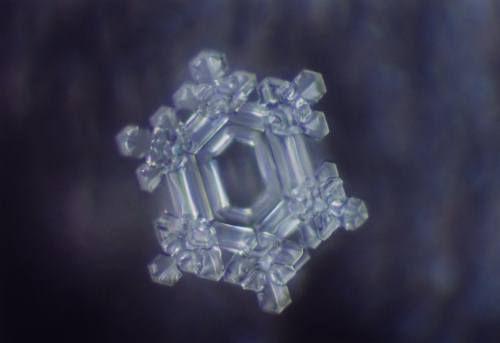
It was 1994 when the idea to freeze water and observe it with microscope came upon me. With this method, I was convinced that I should be able to see something like snow crystals. After two months of trial and error, this idea bore fruit. The beautifully shining hexagonal crystals were created from the invisible world. My staff at the laboratory and I were absorbed in it and began to do many researches.
At first, we strenuously observed crystals of tap water, river water, and lake water. From the tap water we could not get any beautiful crystals. We could not get any beautiful ones from rivers and lakes near big cities, either. However, from the water from rivers and lakes where water is kept pristine from development, we could observe beautiful crystals with each one having its own uniqueness.
The observation was done in various ways:
-
Observe the crystal of frozen water after showing
letters to water -
Showing pictures to water
-
Playing music to water
-
Praying to water
Essentially, Dr. Emoto captured water’s ‘expressions.’ He developed a technique using a very powerful microscope in a very cold room along with high-speed photography, to photograph newly formed crystals of frozen water samples. Not all water samples crystallize however. Water samples from extremely polluted rivers directly seem to express the ‘state’ the water is in.
Dr. Masaru Emoto discovered that crystals formed in frozen water reveal changes when specific, concentrated thoughts are directed toward them. He found that water from clear springs and water that has been exposed to loving words shows brilliant, complex, and colorful snowflake patterns. In contrast, polluted water, or water exposed to negative thoughts, forms incomplete, asymmetrical patterns with dull colors.
The implications of this research create a new awareness of how we can positively impact the earth and our personal health. The success of his books outside Japan has been remarkable. Dr. Emoto has been called to lecture around the world as a result and has conducted live experiments both in Japan and Europe as well as in the US to show how indeed our thoughts, attitudes, and emotions as humans deeply impact the environment.
Water and Music
Natural water
Water and photos

































Water and prayer






Water and prayer
Water and words












“The memory of life arrived on this earth carried by the soul of water. From this memory, life awoke, the human being emerged...”
― Masaru Emoto, Hidden Messages in Water

The beautiful visualization of the numbers of nature
Fractals are probably best known to the general public as the trippy graphics found on Grateful Dead posters. Fractals are marked by self-similarity, a quality defined as showing similar form at all scales of size. I put together a story about fractals found in nature that shows how the numbers show up in nature in everything from rivers to lightning.
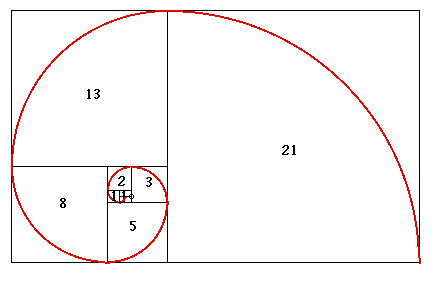
The first nine numbers in the Fibonacci sequence are:
0, 1, 1, 2, 3, 5, 8, 13, 21
The sequence starts with 0 and 1. To find the third number, you add the first and second number. To find the fourth number, you add the second and third number. The fifth number is the the sum of the third and fourth. And so on forever. The tenth number of the sequence is 34, or 13 + 21.
To find any number in the Fibonacci sequence, you just add the preceding two numbers in the sequence. This algorithm sounds simple, and it is, but it also turns out that the Fibonacci sequence is responsible for great complexity—namely a large part of how the natural world is put together. The Fibonacci sequence can be found in the formation of sunflowers, galaxies, cellular structure, hurricanes, and honeybees.

How it works: